This paper aims to explore how to effectively improve managers’ ability to manage time in the university administration process. First, the theoretical knowledge of public management and administrative management is studied. Then, the tomographic analysis is adopted to assess the ability of university administrators to manage their time. Besides, an evaluation index system of university administrators’ operational research time ability is established in line with the evaluation method of university administrative work. In addition, an evaluation model of personal operating research time ability is proposed under the intuitionistic fuzzy analytic hierarchy process (AHP), which optimizes the defects of the original AHP. An improvement plan is given to evaluate team ability in administrative management work. Finally, the evaluators and experts are selected to assess the model. The results demonstrate that the evaluation method reported here can meet the consistency check and accurately output the score ranking of each evaluator under different evaluation indicators and the ability of different managers in different dimensions. In the team total ability score, the highest scores of the four first-level indicators of morality, ability, diligence, and performance in team T1 are 0.1664, 0.1047, 0.0954, and 0.2134, respectively; the highest scores in team T2 are 0.2345, 0.1768, 0.1675, and 0.3243, respectively, outperforming T1. These results indicate that the model established here is also applicable to the management team’s comprehensive operational time capability evaluation. Moreover, suggestions for improving the operational time capability of university administrators are proposed. This paper can provide an effective solution for the ability evaluation of university administrators.
Copyright © 2023 Lie Ma and Jingjing Yu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
In modern colleges and universities, various administrative departments are affected by conventional teaching, teaching and research activities, and teaching auxiliary work in the process of implementing the performance management of colleges and universities. It is difficult to establish an efficient overall operation management model. For cultivating high-quality talents, university administration and public management are the main content of university management [1–2]. Nevertheless, the problems prevailing in the administration of Chinese universities are diverse, such as the diverse sources of administrative personnel and different quality levels [3–4]. In addition, the degree of specialization is low, and the level and skills of modern management need to be improved. The inadequate administrative system of colleges and universities and the lack of training, assessment, promotion, and other mechanisms for managers are the reasons for the poor effectiveness of college administrative management [5]. Whether the executive department of a university can establish a complete performance appraisal index system and whether it can efficiently plan time determines whether it can obtain objective and perfect performance appraisal results. These activities affect whether the compensation plan of each department is fair and reasonable, as well as the work enthusiasm of college staff and the effectiveness of human resources [6]. Therefore, it is essential to rely on scientific practical methods to optimize the administrative management and public management systems of colleges and universities. Common assessment approaches include the analytic hierarchy process (AHP) [7], fuzzy comprehensive evaluation method, management by objectives evaluation method, 360-degree feedback evaluation method [8], and competency performance evaluation method.
Intelligent environments evolved based on a new generation of cyber-physical systems can achieve a high concentration of information resources [8]. For example, distinctive feature extraction methods in deep learning approaches can still be critical for research in various fields [9]. Similarly, in the administration and public management of colleges and universities, intelligent infrastructure and modern human resource management theory and technology are of great significance in breaking the bottleneck of traditional performance evaluation, establishing a scientific and reasonable evaluation index system and personnel ability evaluation system that meets the requirements of modern education and teaching management and personnel training. These measures can promote the reform of the personnel assessment system in colleges and universities, establish an effective administrative system, and improve the ability of administrative personnel to prepare time [10–11]. In addition, the time panning capability in the executive management ability of university managers determines whether managers can distinguish the priorities of their work, arrange their own appointment according to their preferences, and correctly handle the working relationship with others [12–13]. A substantial time management ability can provide practical methods for managers to properly arrange a time, help managers deal with various situations in actual work, and master first-class time management techniques. These behaviors can significantly improve the work efficiency of college management. It is imperative to effectively improve the time management ability of university administrators.
Therefore, it is crucial to promote the ability of time management in the administrative management of colleges and universities. Therefore, this paper studies the connotation of university administration and public management and utilizes AHP to evaluate the ability of university administrators to manage their time. Besides, an evaluation index system is innovatively established for university administrators’ operational research time ability in line with the assessment method of university administrative management work. In addition, the defects of the original AHP are improved to put forward an evaluation model of personal operational research time ability based on the intuitionistic fuzzy analytic hierarchy process (IFAHP). Finally, some evaluators and experts are selected for evaluation via the model, and suggestions for improving the time management ability of university administrative personnel are given. This paper can provide new ideas for the research of university administrative management.
The administrative management system of colleges and universities is a kind of organizational system, mainly including two major administrative management agencies, that is, two kinds of agencies engaged in non-teaching and research activities and teaching and research activities [14–15]. Teaching and scientific research play a leading role in major universities, and administrative management plays a supporting role. However, establishing a university administrative management system can help other administrative personnel implement and complete various management work in universities. Colleges and universities must make full use of all available public resources, adopt flexible working methods, and create a sound system to achieve the assigned educational goals. Administrative work should achieve the preset results and implement its management functions fast and efficiently. The administrative management of colleges and universities involves an extensive range [16]. The high-efficiency operation of colleges and universities is closely related to human resource management. As a critical part of college staff, administrative personnel can reflect the level of personnel management in colleges and universities to a large extent. Performance appraisal is the focus of human resource management in colleges and universities and plays a pivotal role in improving the work efficiency of administrative personnel in colleges and universities. The administrative management of colleges and universities mainly includes three aspects.
Coordinate the relationship between academic research and administration. The relationship between academic and administrative power is the most prominent in the administrative management of colleges and universities. The relationship between administrative leadership, executors, professors, teachers, and students is the key to solving the problem of academic power and administrative power.
Coordinate the relationship between various functions and administrative departments. The various functions that the administrative management of major colleges and universities need to implement also determine the setting of their departments. Therefore, the functions of the administrative management department must be unique and cannot overlap with other departments to ensure the efficiency of administrative management. Formulating scientific and reasonable functions is necessary to ensure the matching of functions and positions.
Coordinate the relationship between reform management and staff structure. Generally speaking, when colleges and universities implement administrative management reform, they need to reform the administrative management team. If the size of the executive management team is excessively large, management will face many problems, which may lead to stagnation in severe cases.
The concept of new public management comes from the United Kingdom, New Zealand, and other countries. It is aimed at the shortcomings of the traditional administrative management model and adopts a theoretical paradigm and a practical paradigm aimed at innovating government management. Higher education is a quasi-public good. The internal management of colleges and universities is a part of higher education, which itself has some attributes of public goods. At present, China is delegating power to colleges and universities. Colleges and universities need to continue the organizational structure, the operating mechanism, and the operating efficiency of the organization and cultivate talents that meet the needs of social development to achieve long-term sustainable development in the market economy. These all coincide with the pursuit of performance mentioned in the core values of new public management. Therefore, administrative management and public management are inseparable in the management of colleges and universities.
AHP combines qualitative and quantitative methods in a research approach to calculate decision weights to solve complicated problems with multiple objectives [17–18]. AHP exploits the experience of decision-makers to discern the relative significance of criteria between measurement objectives. This method also reasonably provides the weight of each standard of each decision-making scheme to acquire the good and bad order of each scheme, which is effectively applied to those problems that are difficult to be solved by quantitative methods. Figure 1 displays the basic rationale and main steps of AHP.

According to Figure 1, a complete AHP usually includes five steps.
Step 1: establish a hierarchical model (as shown in Figure 2).

Figure 2, the AHP model divides the decision-making goals, factors to be considered, and decision-making objects into the highest level (criteria level), the middle level (indicator level), and the lowest level (scheme level) according to the correlation. The highest level comprises the purpose of the decision and the problem to be addressed; the middle level contains elements to be considered and standards for decision-making; the lowest level involves the substitutions when making a decision.
Step 2: construct a judgment matrix for pairwise comparison. Pairwise comparisons between the factors determine the appropriate scale. After building the hierarchical structure, it is required to compare the respective proportions of elements and subordinate indexes. A quantitative scale is also required to complete the transformation from qualitative to quantitative. This process needs to be combined with expert scoring to finally get a judgment matrix table. Suppose that a_ij represents the importance ratio of the ith factor to the jth factor in each level. Then, the judgment matrix A is expressed as Eq. (1) (2) according to the 1-9 scaling method proposed by Professor Saaty.
\[\label{e1}\tag{1} A=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \cdots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right]\]
Step 3: calculate eigenvectors, eigen roots, and weights. The purpose of this step is to calculate the weight value. First, the eigenvector value is solved, obtaining the maximum eigenvalue, which is used for the next consistency check. Specifically, assume that the number of criteria for layer B is expressed as n. Then, the judgment matrix A is normalized to obtain a normalized judgment matrix \({\{ {\bar a_{ij}}\} _{n \times n}}\), where:
\[\label{e2}\tag{2} \bar{a}_{i j}=\frac{a_{i j}}{\sum_{i=1}^n a_{i j}},(j=1,2, \cdots, n)\]
Then, the sum of each row of \({\bar a_{ij}}\) is calculated according to Eq. (3).
\[\label{e3}\tag{3} \omega_i=\sum_{j=1}^n \bar{a}_{i j},(i=1,2, \cdots, n)\]
The vector \(W = {\left( {{\omega _1},{\omega _2}, \cdots ,{\omega _n}} \right)^T}\) is also normalized. Assumes Eq. (4) holds.
\[\label{e4}\tag{4} \omega_1^{(1)}=\frac{\omega_i}{\sum_{j=1}^n \omega_j},(t=1,2, \cdots, n)\]
Then, the relative weight expression of the target layer A to the criterion layer B is written as Eq. (5).
\[\label{e5}\tag{5} {W^{(1)}} = {\left( {{\omega ^{(1)}}_1,{\omega ^{(1)}}_2, \cdots ,{\omega ^{(1)}}_n} \right)^T}\]
Similarly, the relative weights of the indicator layer C to the criterion layer \({B_i}\) is expressed as:
\[\label{e6}\tag{6} \begin{array}{r} W_i^{(2)}=\left(W_{\mathrm{Li}}^{(2)}, W_{2 i}^{(2)}, \cdots, W_{t i}^{(2)}, \cdots, W_{m i}^{(2)}\right)^T \\ \mathrm{i}=1,2, \ldots, \mathrm{n} ; \mathrm{t}=1,2, \ldots, \mathrm{m} ; \end{array}\]
where m represents the number of criteria in the criteria layer \({B_i}\).
Eq. (7) indicates the relative weight of the indicator layer C relative to the criterion layer B.
\[\label{e7}\tag{7} W^{(2)}=\left(W_1^{(2)}, W_2^{(2)}, \cdots, W_t^{(2)}, \cdots, W_n^{(2)}\right)^T\]
Step 4: perform the consistency check analysis. Logical errors may occur when structuring the judgment matrix. For example, A is more important than B, B is more important than C, but C is more important than A. Thus, it is imperative to use consistency checks to check for problems. The consistency check uses the Composite Reliability (CR) value for analysis. If the CR value is less than 0.1, the consistency check is passed. If the CR value is greater than 0.1, the judgment matrix should be appropriately adjusted and then analyzed again. The consistency check process has four steps.
First, the maximum eigenvalue of matrix A is calculated using linear algebra \({{\lambda _{\max }}}\). Then, the index value Consistency Index (CI) of the consistency check is calculated according to Eq. (8).
\[\label{e8}\tag{8} \mathrm{CI}=\frac{\lambda_{\max }-n}{n-1}\]
In Eq. (8), n represents the order of matrix A.
Second, find the consistency index RI. Because objective things are complex and changeable, experts have particular subjectivity and difference in judgment. Only a CI value cannot completely accurately judge whether the matrix A is consistent. Therefore, the average random consistency index proposed by Professor Saaty is introduced here to express the average consistency degree of different matrix orders, RI. Table 1 lists the RI values of the consistency check.
| Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| RI value | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 0.49 |
Finally, the consistency index CR value calculated through Eq. (9).
\[\label{e9}\tag{9} CR = \frac{{CI}}{{RI}}\]
Step 5: analyze the conclusions. If the weights have been derived and the judgment matrix meets the consistency check, a conclusion can be reached, and further analysis can proceed.
The traditional AHP often uses Professor Saaty’s 1-9 scale method. This evaluation process is relatively clear and intuitive and does not require much information. Nevertheless, there are also some defects, such as the subjective cognition of evaluation experts and dependence on life experience. The fuzzy AHP proposed by Buckley (1985) based on the research of Laarhoven and Pedrycz (1983) changed the 1-9 scale representation in the original AHP to be represented by fuzzy numbers and established a fuzzy judgment matrix. Although this can increase objectivity, it is still incomplete.
In the performance evaluation of university administrators, it is necessary to determine the relevant factors of university administrators. Many factors are uncertain, that is, with a certain ambiguity. Besides, no evaluation factor can completely give the boundaries of absolute correctness. Therefore, this paper adopts the IFAHP and uses the intuitionistic fuzzy set for evaluation, quantitatively describes the system without apparent regularity in the objective world, and quantifies the evaluation results. Assume that X represents a domain of discourse. Then, an intuitionistic fuzzy set A on X is expressed as:
\[\label{e10} \begin{aligned} A=\left\{\left\langle x, \mu_A(x), v_A(x)\right\rangle \mid x\right. & \in X\} \\ \mu_A: X & \rightarrow[0,1] \\ v_A: X & \rightarrow[0,1] \end{aligned}\tag{10}\]
where \({{\mu _A}(x)}\) and \({{v_A}(x)}\) respectively represent in the fuzzy set A, the membership and non-membership of the element \(x\) in the set \(X\). Besides, Eq. (11) is satisfied.
\[ 0 \leq \mu_A(x)+v_A(x) \leq 1 \tag{11}\]
The intuition index \({\pi _A}(x)\) of the intuitionistic fuzzy set A is expressed as:
\[\label{e11} \begin{gathered} \pi_A(x)=1-\mu_A(x)-v_A(x) \\ 0 \leq \pi_A(x) \leq 1 \end{gathered}\tag{12}\]
The intuitionistic fuzzy set can comprehensively consider the self-thought process of experts in the evaluation process and the degree of membership, non-membership, and hesitation simultaneously to retain the information of the evaluation process to the greatest extent. The new method is more objective and perfect than the previous AHP. Figure 3 reveals the application process.
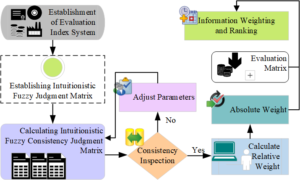
Figure 3 indicates that the process of the IFAHP is similar to that of the traditional AHP. When carrying out the consistency check, first, the intuitionistic fuzzy consistency judgment matrix R- is calculated according to the initial intuition fuzzy judgment matrix \(\bar R – {\left( {{{\bar r}_{ij}}} \right)_{n \times n}}\).
\[ \bar{R}=\left(\bar{r}_{i j}\right)_{n \times n}\tag{13}\]
Rules to follow are:
\[\label{e12}\tag{14} \begin{array}{r} \bar{r}_{i j}=\left(\bar{\mu}_{i j}, \bar{v}_{i j}\right), j>i+1 \\ \bar{r}_{i j}=r_{i j}, j=i+1 \end{array}\]
Eq. (13) holds.
\[\label{e13}\tag{15} \bar{r}_{i j}=\left(\bar{v}_{i j}, \bar{\mu}_{i j}\right), j<i+1\]
where
\[\label{e14}\tag{16} \bar{\mu}_{i j}=\frac{\sqrt[j-i-1]{\prod_{t=i+1}^{j-1} \mu_{i t} \mu_{l j}}}{\sqrt[j-i-1-1]{\prod_{t=i+1}^{j-1} \mu_{i t} \mu_{i j}}+\sqrt[j-i-1-1]{\prod_{i=i+1}^{j-1}\left(1-\mu_{t i}\right)\left(1-\mu_{t j}\right)}}\]
\[\label{e15}\tag{17} \bar{v}_{i j}=\frac{j-i-1 \sqrt{\sqrt{\prod_{t=i+1}^{j-1} v_{i t} v_{i j}}}}{\sqrt[j-i-1-1]{\prod_{t=i+1}^{j-1} v_{i t} v_{i j}}+\sqrt[j-i-1-1]{\sqrt{\prod_{l=i+1}^{j-1}\left(1-v_{i t}\right)\left(1-v_{t j}\right)}}}\]
Then, the consistency check shown in Eq. (16) is used.
\[\label{e16}\tag{18} d(\bar{R}, R)=\frac{1}{2(n-1)(n-2)} \sum_{i=1}^n \sum_{j=1}^n\left(\left|\bar{\mu}_{i j}-\mu_{i j}\right|+\left|\bar{v}_{i j}-v_{i j}\right|+\left|\bar{\pi}_{i j}-\pi_{i j}\right|\right)\]
At the same time, the intuitionistic fuzzy evaluation matrix obtained by combining the expert’s rating on the evaluation scheme constitutes the weighted evaluation information. The weighting and integration of information are carried out using the intuitionistic fuzzy number algorithm.
\[\label{e17} \begin{aligned} & \alpha_1 \oplus \alpha_2=\left(\mu_{\alpha 1}+\mu_{\alpha 2}-\mu_{\alpha 1} \cdot \mu_{\alpha 2}, v_{\alpha 1} \cdot v_{\alpha 2}\right) \\ & \alpha_1 \otimes \alpha_2=\left(\mu_{\alpha 1} \cdot \mu_{\alpha 2}, v_{\alpha 1}+v_{\alpha 2}-v_{\alpha 1} \cdot v_{\alpha 2}\right) \end{aligned}\tag{19}\]
Finally, the score function \(H(\alpha )\) or the sorting function \(\rho (\alpha )\) is selected for the final summary according to the evaluation requirements, which are expressed as:
\[\label{e18}\tag{20} H(\alpha)=\frac{1-v_{i j}}{1+\pi_{i j}}\]
\[\label{e19}\tag{21} \rho(\alpha)=0.5\left(1+\pi_\alpha\right)\left(1-\mu_\alpha\right)\]
The performance evaluation index system of administrative personnel in colleges and universities usually needs to meet several principles: wide coverage, strong versatility, easy to understand, high credibility, scientificity, and other principles. Based on the previous research results, the performance evaluation of administrative personnel in colleges and universities in China is established from four directions: morality, ability, diligence, and performance. These four indicators are regarded as the first-level indicators. The indicators are refined to establish the secondary indicators, forming the evaluation indicator system of the operational research time ability of the administrative personnel in colleges and universities. Table 2 summarizes the details.
| First-level indicator | Numbering | Secondary indicators | Numbering |
|---|---|---|---|
| Morality | A1 | Political morality | B1 |
| Morality | A1 | Professional ethics | B2 |
| Morality | A1 | Psychological morality | B3 |
| Morality | A1 | Ethics | B4 |
| Ability | A2 | Time management ability | B5 |
| Ability | A2 | Organizational management ability | B6 |
| Ability | A2 | Transaction processing capability | B7 |
| Ability | A2 | Creativity | B8 |
| Ability | A2 | Organizational management ability | B9 |
| Diligent | A3 | Work attitude | B10 |
| Diligent | A3 | Sense of responsibility | B11 |
| Diligent | A3 | Effort level | B12 |
| Performance | A4 | Workload | B13 |
| Performance | A4 | Work efficiency | B14 |
| Performance | A4 | Scientific research achievements | B15 |
| Performance | A4 | Earn rewards | B16 |
Then, an individual-level evaluation model of university administrators’ time management ability is established based on the IFAHP according to the situation of individual university administrators’ time management ability in the management process, as shown in Figure 4.
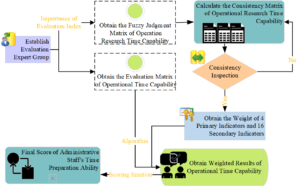
Then, experts in related fields are invited to compare and judge the indicators in the indicator system and score the performance of the university administrators under each indicator. Expert judgment is combined with evaluation matrix processing to obtain the score of the evaluated person’s operational time capability. Three senior managers who have been engaged in the administration of colleges and universities for more than 30 years in a city for evaluation and scoring were selected as the members of the expert group. Six administrative management practitioners (numbered H1 H6) who have performed well in their work in a university were chosen as evaluation objects to evaluate their operational time ability.
First, let experts study and discuss the importance of the indicator system established above. Table 3 Table 7 summarize the scoring results obtained by pairwise comparison.
| A1 | A2 | A3 | A4 |
|---|---|---|---|
| (0.49,0.29) | (0.20,0.75) | (0.39,0.45) | (0.39,0.45) |
| (0.79,0.15) | (0.49,0.29) | (0.39,0.45) | (0.59,0.25) |
| (0.59,0.25) | (0.59,0.25) | (0.49,0.29) | (0.79,0.15) |
| (0.59,0.25) | (0.39,0.45) | (0.20,0.75) | (0.49,0.29) |
| B1 | B2 | B3 | B4 |
|---|---|---|---|
| (0.49,0.30) | (0.19,0.75) | (0.39,0.44) | (0.39,0.44) |
| (0.80,0.15) | (0.49,0.30) | (0.39,0.44) | (0.60,0.25) |
| (0.60,0.25) | (0.60,0.25) | (0.49,0.30) | (0.80,0.15) |
| (0.60,0.25) | (0.39,0.44) | (0.19,0.75) | (0.49,0.30) |
| (0.59,0.25) | (0.39,0.45) | (0.20,0.75) | (0.49,0.29) |
| B5 | B6 | B7 | B8 | B 9 |
|---|---|---|---|---|
| (0.49,0.28) | (0.20,0.75) | (0.28,0.60) | (0.40,0.45) | (0.40,0.45) |
| (0.79,0.15) | (0.49,0.28) | (0.79,0.15) | (0.70,0.20) | (0.60,0.24) |
| (0.70,0.20) | (0.20,0.75) | (0.49,0.28) | (0.28,0.60) | (0.60,0.24) |
| (0.60,0.24) | (0.28,0.60) | (0.70,0.20) | (0.49,0.28) | (0.28,0.60) |
| (0.60,0.24) | (0.40,0.45) | (0.40,0.45) | (0.70,0.20) | (0.49,0.28) |
| B10 | B11 | B12 |
|---|---|---|
| (0.49,0.29) | (0.29,0.60) | (0.20,0.75) |
| (0.70,0.20) | (0.49,0.29) | (0.10,0.88) |
| (0.80,0.15) | (0.88,0.10) | (0.49,0.29) |
| B13 | B14 | B15 | B16 |
|---|---|---|---|
| (0.49,0.28) | (0.29,0.59) | (0.19,0.74) | (0.39,0.44) |
| (0.69,0.19) | (0.49,0.29) | (0.10,0.88) | (0.70,0.19) |
| (0.79,0.20) | (0.89,0.10) | (0.49,0.28) | (0.28,0.60) |
| (0.69,0.28) | (0.28,0.59) | (0.74,0.22) | (0.49,0.28) |
Then, the experts mentioned above who have not yet experienced management were invited to evaluate the performance of the six administrators under different indicators. The arithmetic average of the scores of the three experts was used as the final evaluation result. The final data of the fuzzy evaluation matrix of the operational research time ability of university administrators are shown in Table 8.
| \(w_{1j}^{(2)}\) | \(w_{2j}^{(2)}\) | \(w_{3j}^{(2)}\) | \(w_{4j}^{(2)}\) | \(w_{5j}^{(2)}\) | \(w_{6j}^{(2)}\) |
|---|---|---|---|---|---|
| (0.25,0.56) | (0.40,0.62) | (0.22,0.75) | (0.46,0.57) | (0.04,0.92) | (0.07,0.90) |
| (0.74,0.26) | (0.46,0.52) | (0.09,0.90) | (0.86,0.04) | (0.22,0.70) | (0.42,0.58) |
| (0.46,0.44) | (0.49,0.42) | (0.44,0.50) | (0.49,0.49) | (0.49,0.59) | (0.58,0.40) |
| (0.52,0.49) | (0.40,0.65) | (0.42,0.48) | (0.05,0.90) | (0.40,0.52) | (0.02,0.92) |
| (0.24,0.65) | (0.08,0.89) | (0.24,0.65) | (0.79,0.22) | (0.60,0.42) | (0.50,0.42) |
| (0.27,0.72) | (0.22,0.70) | (0.25,0.70) | (0.54,0.44) | (0.24,0.78) | (0.54,0.46) |
| (0.45,0.40) | (0.42,0.52) | (0.44,0.64) | (0.74,0.24) | (0.24,0.65) | (0.42,0.47) |
| (0.44,0.52) | (0.08,0.90) | (0.28,0.70) | (0.46,0.52) | (0.65,0.22) | (0.84,0.22) |
| (0.26,0.80) | (0.42,0.60) | (0.46,0.50) | (0.22,0.79) | (0.24,0.77) | (0.44,0.58) |
| (0.27,0.65) | (0.06,0.90) | (0.48,0.45) | (0.94,0.02) | (0.26,0.70) | (0.60,0.44) |
| (0.92,0.04) | (0.02,0.94) | (0.22,0.78) | (0.68,0.26) | (0.27,0.62) | (0.74,0.22) |
| (0.04,0.92) | (0.40,0.57) | (0.22,0.72) | (0.54,0.44) | (0.94,0.02) | (0.07,0.88) |
| (0.24,0.78) | (0.42,0.48) | (0.40,0.66) | (0.64,0.22) | (0.40,0.60) | (0.42,0.60) |
| (0.50,0.50) | (0.46,0.62) | (0.49,0.52) | (0.64,0.27) | (0.97,0.02) | (0.57,0.45) |
| (0.92,0.02) | (0.24,0.79) | (0.44,0.62) | (0.40,0.52) | (0.80,0.22) | (0.54,0.42) |
| (0.70,0.24) | (0.24,0.72) | (0.24,0.75) | (0.42,0.55) | (0.82,0.08) | (0.85,0.02) |
In Table 8, the larger the value of \({\bar u_{ij}}\), the greater the degree of membership of the administrator to this index; the smaller the value of \({\bar v_{ij}}\), the smaller the degree of non-membership of the administrator under this index. These indicate that the manager being evaluated has a higher degree of fit with the indicators in the evaluation system. The evaluation matrix is used as a backup and brought into the formula of the consistency check above to obtain the consistency check matrix as follows:
\[\label{e20}\tag{22} \bar{R}_1=\left[\begin{array}{lll} (0.4987,0.2998) & (0.3000,0.6000) & (0.1320,0.8249) \\ (0.6714,0.2271) & (0.4987,0.3000) & (0.1000,0.8997) \\ (0.8521,0.1064) & (0.8997,0.1000) & (0.4987,0.3998) \end{array}\right]\]
\[\label{e21}\tag{23} \bar{R}_2=\left[\begin{array}{lll} (0.7865,0.2998) & (0.7865,0.6000) & (0.1320,0.8249) \\ (0.6714,0.2271) & (0.4987,0.3000) & (0.0999,0.9000) \\ (0.8521,0.1064) & (0.8997,0.1000) & (0.4987,0.2998) \end{array}\right]\]
Then, the relative weights of each level of indicators are calculated, and the weights of each level of indicators are multiplied to obtain the total weight.
\[\label{e22} \begin{aligned} & \omega_1^{(1)}=\omega^{(1)} A_1 \otimes \omega^{(1)} B_1=(0.0235,0.9105) \\ & \omega_2^{(1)}=\omega^{(1)} A_1 \otimes \omega^{(1)} B_2=(0.0352,0.9347) \\ & \omega_3^{(1)}=\omega^{(1)} A_1 \otimes \omega^{(1)} B_3=(0.0395,0.9436) \\ & \omega_4^{(1)}=\omega^{(1)} A_1 \otimes \omega^{(1)} B_4=(0.0237,0.9109) \\ & \omega_5^{(1)}=\omega^{(1)} A_1 \otimes \omega^{(1)} B_5=(0.0380,0.9405) \\ & \omega_6^{(1)}=\omega^{(1)} A_2 \otimes \omega^{(1)} B_6=(0.0258,0.9566) \\ & \omega_7^{(1)}=\omega^{(1)} A_2 \otimes \omega^{(1)} B_7=(0.0482,0.9760) \\ & \omega_8^{(1)}=\omega^{(1)} A_2 \otimes \omega^{(1)} B_8=(0.0279,0.9584) \end{aligned}\tag{24}\]
Then, the personal evaluation information of the university administrators obtained above is converted into the specific score of the operational time ability for the subsequent analysis. Figure 5 presents the ability scores of the six administrative staff.
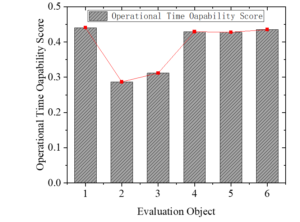
According to Figure 5, among the six university administrators who participated in the scoring, the appraisee with the number of “H1” scored the highest, and the operational time capability score was 0.4409; the lowest score was 0.2871 for the evaluated person numbered “H2”. The final ability ranking is H1>H4>H5>H6>H3>H2. It can be seen that although they are all engaged in the administrative work of colleges and universities, their ability in time management is quite different. The above scoring function is used to calculate the evaluation results of different evaluated values in each index to evaluate their ability, as shown in Figure 6.

Figure 6 suggests that from the perspective of index B1, the order of scores from high to low is H6>H4>H1>H2>H3>H5. Similarly, the score ranking of each evaluator under other indicators can be obtained. From the perspective of each evaluation value, taking the evaluator H1 as an example, the scores of different indicators are not the same. The lowest-ranking indicators are B9, B12, and B13, respectively. These three indicators represent organizational management ability, effort level, and workload, respectively. Although the overall score of the assessed H1 is high, these three abilities are relatively weak, which are also weak in the ability to prepare time and need to be strengthened in daily administration. Similarly, the ability of other managers in different dimensions can be analyzed.
This paper studies the content of administrative management and public management in colleges and universities to establish an effective performance appraisal method to improve their ability to manage time. Therefore, the AHP method is chosen to analyze the performance evaluation indicators of university administrators. AHP is suitable for analyzing and discussing unquantifiable goals. The administrative work in colleges and universities is complicated and difficult to quantify. Therefore, this paper proposes an IFAHP model after optimizing the original AHP. First, an evaluation index system is established for the operational time ability of administrative personnel in colleges and universities. Then, an evaluation model of personal operational time capability is established based on IFAHP to evaluate the time management capability of university administrators. Solutions are also given for the comprehensive capability assessment of the management team. Finally, suggestions for improving the time management ability of university administrators are given. Proposing suggestions to improve the time management ability of college administrators is significant to the future development of college administration.
Nevertheless, this paper still has some limitations, such as the number of administrative staff involved in the evaluation and the small number of experts involved in the scoring used in the study, which may lead to partisan bias in the data results. Therefore, future research will increase the scope of investigation and evidence collection of administrative management work to improve the evaluation system.